Co to jest liczba rzeczywista?

Czym są liczby rzeczywiste? Jakie liczby znajdują się w zbiorze liczb rzeczywistych? Aby lepiej zrozumieć tę ważną wiedzę matematyczną, prosimy o przeczytanie poniższego artykułu.

Liczba rzeczywista

• 1. Co to jest liczba rzeczywista?
• 2. Oś liczb rzeczywistych
•  3. Porównaj liczby rzeczywiste
• 3. Własności zbioru liczb rzeczywistych
• 4. Wartość bezwzględna liczby rzeczywistej
• 5. Przykładowe ćwiczenia na liczbach rzeczywistych

1. Co to jest liczba rzeczywista?

• Liczby rzeczywiste to zbiór liczb wymiernych i niewymiernych.
• Zbiór jest symbolem zbioru liczb rzeczywistych, składającego się z liczb rzeczywistych.

• Liczba wymierna to liczba zapisana w postaci ułamka (a, b ∈ Z, b ≠ 0). Na przykład 
• Zbiór liczb wymiernych oznaczamy symbolem 
• Liczba niewymierna to nieskończona, niepowtarzalna liczba dziesiętna. Na przykład:
• Zbiór liczb niewymiernych oznaczamy symbolem 

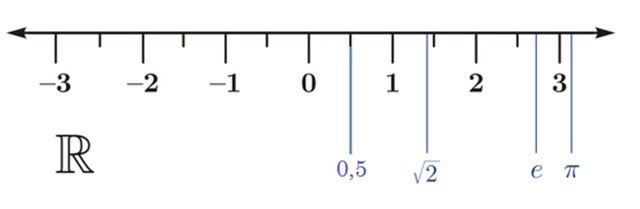
Zbiór liczb rzeczywistych pokrywa oś liczbową.

Na przykład:

2. Oś liczb rzeczywistych

Każda liczba rzeczywista jest reprezentowana przez punkt na osi liczbowej.

• Natomiast każdy punkt na osi liczbowej przedstawia liczbę rzeczywistą.
• Tylko zbiór liczb rzeczywistych wypełnia oś liczbową.

 3. Porównaj liczby rzeczywiste

Metoda

• Dla dowolnych dwóch liczb rzeczywistych x, y zawsze mamy x = y lub x < y lub x > y
• Liczby rzeczywiste większe od 0 nazywane są dodatnimi liczbami rzeczywistymi, a liczby rzeczywiste mniejsze od 1 nazywane są ujemnymi liczbami rzeczywistymi. Liczba 0 nie jest liczbą rzeczywistą ani dodatnią, ani ujemną.
• Porównywanie dodatnich liczb rzeczywistych jest podobne do porównywania liczb wymiernych.
• Ponieważ a, b są dwiema dodatnimi liczbami rzeczywistymi, to jeżeli a > b, to .

Przykład: Wpisz odpowiednią cyfrę w kwadracie:

Przewodnik po rozwiązaniach

a) -7,5(0)8 > -7,513

b) -3,02 <>

c) -0,4(9)854 <>

d) -1,(9)0765 <>

Przykład: Uporządkuj liczby rzeczywiste: od najmniejszej do największej

Przewodnik po rozwiązaniach

Uporządkuj liczby rzeczywiste od najmniejszej do największej:

Na przykład: Udowodnij, że:

Dla a, b są dwiema dodatnimi liczbami rzeczywistymi, jeżeli a > b, to

Przewodnik po rozwiązaniach

Jeśli a > b, to

a, b to dwie dodatnie liczby rzeczywiste, więc a + b > 0

Jeżeli a > b to a – b > 0

Rozważ produkt

Ponieważ a2 – b2 > 0

=> a2 > b2 => dpcm

3. Własności zbioru liczb rzeczywistych

W zbiorze tym definiujemy również działania dodawania, odejmowania, mnożenia, dzielenia, potęgowania, pierwiastkowania kwadratowego... A w działaniach liczby rzeczywiste mają te same własności, co działania w zbiorze liczb wymiernych.

W zbiorze liczb rzeczywistych działania mają następujące własności w odniesieniu do mnożenia:

• Dla wszystkich nieruchomości:
• Dodaj 0: 
• Własność przemienna: ;
• Połączone właściwości: 
• Własność przemienna: a. b = b. A
• Własności asocjacyjne: (a. b). c = a. (p.n.e.)
• Właściwości mnożenia przez liczbę 1:
• Prawo rozdzielności mnożenia względem dodawania: a. (b + c) = a. b + a. C
• Dla każdej liczby rzeczywistej a ≠ 0 istnieje liczba odwrotna taka, że

- Oznacza to, że powyższe obliczenia mają również własności przemienne i łącznościowe, podobnie jak inne zbiory liczb. To samo dotyczy odejmowania, mnożenia, dzielenia…

Relacja między zbiorami liczb

Na przykład: Wykonaj obliczenie:

Przewodnik po rozwiązaniach

Na przykład: Znajdź x, wiedząc:

Przewodnik po rozwiązaniach

4. Wartość bezwzględna liczby rzeczywistej

Definicja: Odległość od punktu a do punktu 0 na linii liczbowej jest wartością bezwzględną liczby a (a jest liczbą rzeczywistą). Wartość bezwzględna liczby ujemnej jest taka sama jak ona sama, wartość bezwzględna liczby ujemnej jest jej przeciwieństwem.

Przegląd:

• Jeśli
• Jeśli
• Jeśli
• Jeśli

Natura

• Wartość bezwzględna każdej liczby jest nieujemna.
• Ogólne: dla wszystkich a ∈ R

Swoiście:

Niektóre właściwości

- Dwie liczby, które są równe lub przeciwne, mają równą wartość bezwzględną i odwrotnie, dwie liczby, które mają równą wartość bezwzględną, są równe lub przeciwne.

Przegląd:

- Każda liczba jest większa lub równa przeciwstawnej wartości swojej wartości bezwzględnej i jednocześnie mniejsza lub równa swojej wartości bezwzględnej.

Przegląd: i

- Spośród dwóch liczb ujemnych, mniejsza ma większą wartość bezwzględną.

Przegląd: Jeśli

- Spośród dwóch liczb dodatnich, mniejsza ma mniejszą wartość bezwzględną.

Przegląd: Jeśli

- Wartość bezwzględna iloczynu jest równa iloczynowi wartości bezwzględnych.

Przegląd:

- Wartość bezwzględna ilorazu jest równa ilorazowi dwóch wartości bezwzględnych.

Przegląd:

5. Przykładowe ćwiczenia na liczbach rzeczywistych

Przykład 1: Uzupełnij luki odpowiednimi symbolami ∈, ∉, ⊂ (…):

3 …. Q; 3 …. R ; 3… ja ; -2,53… P;

0,2(35) …. I ; N …. Z ; I …. R.

Polecić

a) 3 ∈ Q ; 3 ∈ R ; 3 ∉ ja ; -2,53 ∈ Q

b) 0,2(35) ∉ 2; N ∈ Z ; Ja ⊂R

Przykład 2: Znajdź zbiory

a) Q ∩ I ;
b) R ∩ I.

Polecić

a) Q ∩ I = Ø ;
b) R ∩ I = I.

Przykład 3: Wpisz odpowiednią cyfrę w (…) 

a) – 3,02 < –="" 3,="" …="">

b) – 7,5 … 8 > – 7,513

c) – 0,4 … 854 < –="">

d) -1, … 0765 < –="">

Polecić

a) – 3,02 < –="">
b) – 7,508 > – 7,513 ;
c) – 0,49854 < –="" 0,49826="">
d) -1,90765 < –="">

Przykład 4: Znajdź x, wiedząc:

3,2.x + (-1,2).x +2,7 = -4,9;

Polecić

3.2. x + (-1,2).x + 2,7 = -4,9

[3,2 + (-1,2)].x + 2,7 = -4,9.

2,x + 2,7 = – 4,9.

2.x = – 4,9 – 2,7

2.x = – 7,6

x = -7,6 : 2

x = -3,8

Oprócz liczb rzeczywistych możesz dowiedzieć się więcej o innych definicjach matematycznych, takich jak liczby kwadratowe , liczby niewymierne, liczby wymierne , liczby pierwsze , liczby naturalne ...