Co to jest liczba wymierna? Co to jest liczba niewymierna?

Definicje i wzory liczb wymiernych i niewymiernych stanowią istotną wiedzę matematyczną, którą uczniowie muszą zrozumieć, aby zdobyć solidne podstawy matematyczne. W poniższym artykule przedstawiono definicję, własności i formy matematyczne liczb wymiernych i niewymiernych. Proszę się z tym zapoznać.

Liczby wymierne, liczby niewymierne

• Co to jest liczba wymierna?
  • Klasyfikacja liczb wymiernych
  • Przedstawianie liczb wymiernych na osi liczbowej
  • Dodawanie i odejmowanie liczb wymiernych
  • Mnożenie i dzielenie liczb wymiernych
  • Wartość bezwzględna liczby wymiernej
  • Porównaj dwie liczby wymierne
  • Wzór na obliczenie potęgi liczby wymiernej
• Co to jest liczba niewymierna?
  • Pojęcie liczb niewymiernych
  • Właściwości liczb niewymiernych
• Jaka jest różnica między liczbami wymiernymi i niewymiernymi?
• Relacje zbiorów liczb
• Ćwiczenia z liczb wymiernych

Co to jest liczba wymierna?

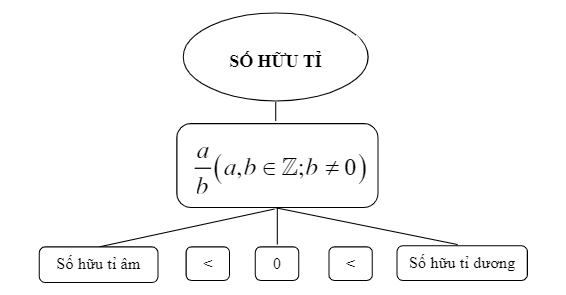
- Liczby wymierne to zbiór liczb, które można zapisać w postaci ułamków (ilorazów). Oznacza to, że liczbę wymierną można przedstawić za pomocą nieskończonego ułamka dziesiętnego okresowego.

- Liczby wymierne zapisuje się jako , gdzie a i b są liczbami całkowitymi, ale b musi być różne od 0.

- jest zbiorem liczb wymiernych.

=> Zbiór liczb wymiernych: .

Na przykład: , , … są liczbami wymiernymi.

• Każda liczba całkowita a jest liczbą wymierną, ponieważ można ją zapisać w postaci .

Na przykład: Mamy liczby wymierne.

Mamy:

Komentarz: wszystkie są liczbami wymiernymi.

Klasyfikacja liczb wymiernych

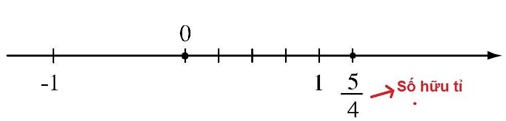
Liczby wymierne dzielą się na dwa typy: liczby wymierne ujemne i liczby wymierne dodatnie. Swoiście:

• Liczby wymierne ujemne: obejmują liczby wymierne mniejsze od 0.
• Liczby wymierne dodatnie: obejmują liczby wymierne większe od 0.

Uwaga: Liczba 0 nie jest ani ujemną, ani dodatnią liczbą wymierną.

Natura

• Zbiór liczb wymiernych jest zbiorem przeliczalnym.
• Własność przemienna:
• Właściwość dodawania z 0:
• Połączone właściwości:

Przedstawianie liczb wymiernych na osi liczbowej

- Aby przedstawić liczby wymierne na osi liczbowej, stosujemy następujące czynniki:

Krok 1: Zapisz liczbę wymierną jako ułamek

Krok 2: Podziel odcinek jednostkowy na b równych części, aby uzyskać nowy odcinek jednostkowy, który jest starą jednostką.

Krok 3: Liczbę wymierną przedstawiamy za pomocą punktu A, który jest odległością nowej jednostki od punktu 0.

• Jeżeli 0 jest liczbą ujemną, to A znajduje się na lewo od 0.
• Jeżeli A jest liczbą dodatnią, to znajduje się na prawo od 0.

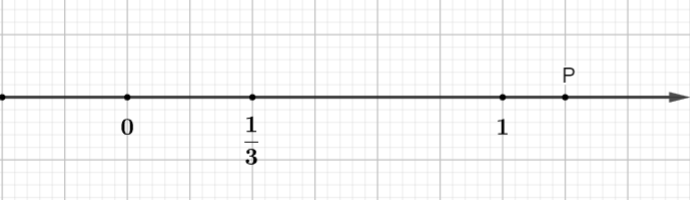
Na przykład: Na rysunku punkt P przedstawia liczbę wymierną:

Polecić

Odcinek jednostkowy jest podzielony na 6 równych części (nowa jednostka stanowi 1/6 starej jednostki)

Punkt P znajduje się w odległości 7 nowych jednostek od punktu O.

A punkt P leży na prawo od punktu O, więc P jest dodatnią liczbą wymierną.

Zatem P reprezentuje liczbę wymierną.

Dodawanie i odejmowanie liczb wymiernych

i) Reguły dodawania i odejmowania dwóch liczb wymiernych

Możemy dodawać i odejmować dwie liczby wymierne x i y, zapisując je jako dwa ułamki i stosując reguły dodawania i odejmowania ułamków.

U nas znajdziesz:

ii) Właściwości

- Dodawanie liczb wymiernych ma takie same własności jak dodawanie ułamków: przemienność, łączność, dodawanie z 0, dodawanie z liczbami przeciwnymi.

- Mamy:

a) Własność przemienna:

b) Własności asocjacyjne:

c) Dodaj 0:

d) Dodaj liczbę przeciwną:

iii, Zasady przejściowe

Przenosząc wyraz z jednej strony równania na drugą, musimy zmienić znak tego wyrazu.

W Q mamy sumę algebraiczną, w której możemy zamieniać wyrazy, umieszczać nawiasy w celu grupowania wyrazów w sposób dowolny, jak w przypadku sum algebraicznych w zbiorze liczb całkowitych.

• Z jeśli wtedy
• U nas znajdziesz:

Mnożenie i dzielenie liczb wymiernych

i) Zasady mnożenia i dzielenia dwóch liczb wymiernych

- Możemy mnożyć i dzielić dwie liczby wymierne, zapisując je jako ułamki zwykłe, a następnie stosując reguły mnożenia i dzielenia ułamków zwykłych.

• U nas znajdziesz:
• U nas znajdziesz:

Na przykład:

Mnożenie liczb wymiernych: 

Podziel liczby wymierne: 

ii) Właściwości

- Mnożenie liczb wymiernych ma te same własności co mnożenie ułamków: przemienność, łączność, mnożenie przez 1 i rozdzielność mnożenia względem dodawania.

- Każda liczba wymierna różna od zera ma liczbę odwrotną.

- Mamy:

• Własność przemienna: .
• Właściwości asocjacyjne: .
• Własność mnożenia przez 1: .
• Właściwości rozdzielcze: .
• Z . Odwrotnością a jest .

Wartość bezwzględna liczby wymiernej

- Wartość bezwzględna liczby wymiernej a, oznaczana jako , jest odległością punktu a od punktu 0 na osi liczbowej.

Na przykład:

(Ponieważ )

(Ponieważ )

Porównaj dwie liczby wymierne

- Dla dowolnych 2 liczb wymiernych zawsze mamy albo, albo.

- Aby porównać dwie liczby wymierne wykonujemy następujące czynności:

• Zapisz jako 2 ułamki o tym samym dodatnim mianowniku:
• Porównaj liczniki jako liczby całkowite a, b:

Na przykład: Porównaj dwie liczby wymierne: i

Mamy:

Ponieważ jest dobre.

Wzór na obliczenie potęgi liczby wymiernej

Wzory do obliczania potęg liczb wymiernych, które musisz zapamiętać

• Iloczyn dwóch potęg o tej samej podstawie:
• Moc mocy
• Moc produktu
• Potęga ilorazu

Co to jest liczba niewymierna?

Pojęcie liczb niewymiernych

• Mówiąc o liczbach wymiernych, nie sposób nie wspomnieć o liczbach niewymiernych. Są to liczby zapisane w postaci nieskończonych, niepowtarzalnych cyfr dziesiętnych, oznaczanych symbolem .
• Liczb rzeczywistych, które nie są liczbami wymiernymi, nie można przedstawić w postaci ilorazów.

Na przykład: 3,145248… jest liczbą niewymierną.

Właściwości liczb niewymiernych

Zbiór liczb niewymiernych jest zbiorem nieprzeliczalnym.

Na przykład:

Liczby niewymierne: 0,1010010001000010000010000001… (jest to nieskończona, niepowtarzalna liczba dziesiętna)

Liczba pierwiastków kwadratowych: √2 (pierwiastek kwadratowy)

Pi (π): 3,14159 26535 89793 23846 26433 83279 50 288…..

Jaka jest różnica między liczbami wymiernymi i niewymiernymi?

• Liczby wymierne obejmują nieskończone ułamki dziesiętne okresowe, natomiast liczby niewymierne to nieskończone nieokresowe ułamki dziesiętne.
• Liczby wymierne to po prostu ułamki, podczas gdy liczby niewymierne dzielą się na wiele różnych typów.
• Liczby wymierne to liczby policzalne, natomiast liczby niewymierne to liczby niepoliczalne.

Relacje zbiorów liczb

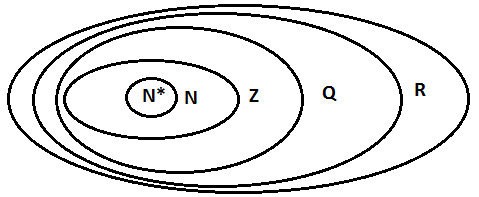
Symbole zbiorów liczb:

• N: Zbiór liczb naturalnych
• N*: Zbiór liczb naturalnych różnych od 0
• Z: Zbiór liczb całkowitych
• P: Zbiór liczb wymiernych
• I: Zbiór liczb niewymiernych

Mamy: R = Q ∪ I.

Zestaw N; Z ; Q; R.

Wówczas relacja inkluzji pomiędzy zbiorami liczb jest następująca: N ⊂ Z ⊂ Q ⊂ R

Ćwiczenia z liczb wymiernych

Formularz 1: Wykonaj obliczenia obejmujące liczby wymierne

Metoda rozwiązania: Aby rozwiązać zadania dotyczące wykonywania obliczeń na liczbach wymiernych, najpierw zamień liczby wymierne na ułamki, a następnie zastosuj reguły obliczeń dotyczące dodawania, odejmowania, mnożenia i dzielenia liczb wymiernych.

Przykład: Oblicz  

Odpowiedź:

Formularz 2: Przedstawianie liczb wymiernych na osi liczbowej

Rozwiązanie: Należy ustalić, czy liczba wymierna jest liczbą wymierną dodatnią czy ujemną, a następnie wykonać kolejne kroki:

• Jeśli liczba wymierna a/b jest dodatnią liczbą wymierną: Na osi liczbowej, w kierunku dodatnim, podziel długość 1 jednostki na b równych części. Następnie wybierz punkt leżący na dodatnim kierunku osi Ox, wskaż część i określ położenie liczby wymiernej a/b.
• Jeśli liczba wymierna a/b jest ujemną liczbą wymierną: Na osi liczbowej, w kierunku ujemnym osi, podziel długość 1 jednostki na b równych części. Następnie wybierz punkt leżący na kierunku ujemnym osi Ox, wskaż część i określ położenie liczby wymiernej a/b.

Formularz 3: Porównywanie liczb wymiernych

Rozwiązanie: Zamień podane liczby wymierne na ułamki o takim samym dodatnim mianowniku, a następnie porównaj liczniki. Bardziej zaawansowane równania możemy porównywać z ułamkami pośrednimi, aby znaleźć odpowiedź.

Formularz 4: Określ, czy liczba wymierna jest ujemna, dodatnia czy równa 0

Metoda rozwiązania: Aby rozwiązać zadania typu 4, uczniowie muszą wykorzystać własności liczb wymiernych, aby określić, czy dana liczba wymierna jest ujemna, dodatnia czy 0.

Na przykład: Mając daną liczbę wymierną x = (a – 25)/29, określ wartość a tak, aby:

• x jest ujemne
• x jest dodatnie
• x = 0

Odpowiedź:

x jest liczbą ujemną => (a – 25)/29 < 0=""> a – 25 < 0=""> a <>

x jest liczbą dodatnią => (a – 25)/29 > 0 => a – 25 > 0 => a > 25

x = 0 => (a – 25)/29 = 0 0 => a – 25 = 0 => a = 25

Formularz 5: Znajdź liczby wymierne w przedziale zgodnie z podanymi warunkami

Rozwiązanie: Jeśli pytanie wymaga znalezienia liczb wymiernych w przedziale zgodnie z podanymi warunkami, musimy umieścić liczby wymierne w tym samym liczniku lub mianowniku, aby znaleźć odpowiedź.

Przykład: Znajdź wartość m dla wartości większej niż i mniejszej niż

Przewodnik po odpowiedziach

Zamień ułamki na wspólne mianowniki w następujący sposób:

Wspólny mianownik: 18

Zgodnie z pytaniem, które mamy:

Formularz 6: Znajdź x przy użyciu liczb wymiernych

Metoda rozwiązywania problemów matematycznych: Aby znaleźć x przy użyciu liczb wymiernych, należy wykonać redukcję do wspólnego mianownika i zamienić x na jedną stronę, a pozostałe wyrazy na 1. Następnie obliczyć wartość x

Na przykład: Znajdź x znając x. (2/ 3) + 5/ 6 = 1/ 8

Odpowiedź:

X . (2/ 3) + 5/ 6 = 1/ 8

=> x. (2/ 3) = 1/ 8 + 5/ 6

=> x = 46/ 48 : 2/ 3

=> x = 23 . 3 / 24 . 2

=> 23/16

Formularz 7: Znajdź a tak, aby wyrażenie było liczbą całkowitą

Metoda rozwiązywania zadań matematycznych: W przypadku problemu znalezienia a, jeśli licznik nie zawiera a, musimy posłużyć się znakiem podzielności. Jeżeli licznik zawiera znak a, należy użyć znaku podzielności lub oddzielić licznik od mianownika. Jeżeli zadanie wymaga jednoczesnego znalezienia a i b, pogrupuj a lub b i przekształć je w postać ułamkową w celu wykonania obliczeń.

Przykład: Znajdź liczbę całkowitą a, pod warunkiem że 8/(a – 1) jest liczbą całkowitą

Odpowiedź:

Warunek: a – 1 ≠ 0 => a ≠ 1

Niech a będzie liczbą całkowitą => 8 jest podzielne przez (a – 1)

=> (a – 1) jest czynnikiem 8 => U(8) = {-8, -4, -2, -1, 1, 2, 4, 8}

=> (a – 1) = {-8, -4, -2, -1, 2, 4, 8}

=> a = {-7, -3, -1, 0, 3, 5, 9}

Mam nadzieję, że powyższy artykuł pomógł Ci zrozumieć, czym są liczby wymierne, czym są liczby niewymierne, jakie są rodzaje liczb wymiernych, czym są symbole liczb wymiernych oraz jak rozpoznawać liczby wymierne, aby łatwo rozwiązywać problemy.

Oprócz wiedzy o liczbach niewymiernych i wymiernych podanej powyżej, możesz odwołać się do innej wiedzy matematycznej, takiej jak ułamki , liczby mieszane , liczby dziesiętne ...