Wzór na obliczanie wysokości w trójkątach foremnych, równoramiennych, równobocznych i prostokątnych

Wysokość w trójkącie jest linią prostą o ważnych własnościach i jest ściśle związana z zagadnieniami geometrii płaskiej. Jaka jest wysokość i jak obliczyć wysokość w trójkącie? Odpowiedź i najprostszy wzór na obliczenie wysokości trójkąta znajdziesz w artykule poniżej.

Spis treści

• Wzór na obliczenie wysokości w trójkącie
  • Oblicz wysokość w trójkącie foremnym
  • Oblicz wysokość w trójkącie równobocznym
  • Wzór na obliczenie wysokości w trójkącie prostokątnym
  • Wzór na obliczenie wysokości w trójkącie równoramiennym
• Definicja wysokości w trójkącie
• Właściwości trzech wysokości trójkąta

Wzór na obliczenie wysokości w trójkącie

Oblicz wysokość w trójkącie foremnym

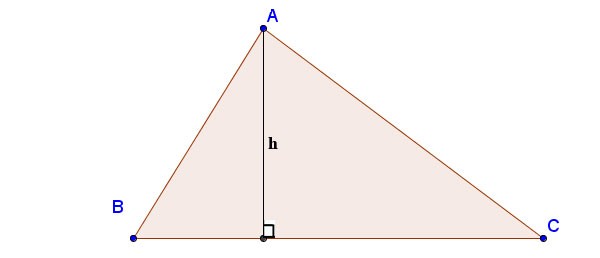
Jak obliczyć wysokość trójkąta za pomocą wzoru Herona:

Gdzie a, b, c są długościami boków; ha jest wysokością poprowadzoną od wierzchołka A do boku BC; p jest półobwodem:

Na przykład: 

Dany jest trójkąt ABC, bok AB = 4 cm, bok BC = 7 cm, bok AC = 5 cm. Oblicz wysokość AH z punktu A przecinającego BC w punkcie H i oblicz pole trójkąta ABC.

Nagroda:

Połowa obwodu trójkąta: P = (AB + BC + AC) : 2 = (4 + 7 + 5) : 2 = 8(cm)

Wysokość   

=>

Rozważmy trójkąt ABC. Mamy:

Więc,

Oblicz wysokość w trójkącie równobocznym

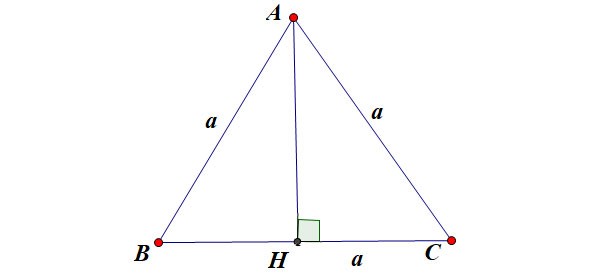
Załóżmy, że trójkąt równoboczny ABC ma bok długości a, jak pokazano na rysunku:

Tam:

• h jest wysokością trójkąta równobocznego
• a jest długością boku trójkąta równobocznego

Wzór na obliczenie wysokości w trójkącie prostokątnym

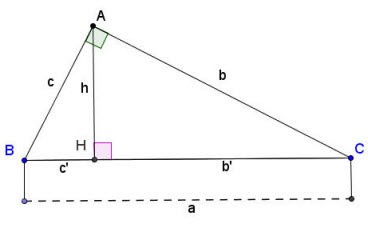
Załóżmy, że istnieje trójkąt prostokątny ABC, który dokładnie w punkcie A jest pokazany powyżej:

Wzór na obliczanie boków i wysokości w trójkącie prostokątnym:

1.a2 = b2 + c2

2. b2 = ab′ i c2 = ac′

3. ah = bc

4. h2 = b′.c'

5.

Tam:

• a, b, c to boki trójkąta prostokątnego pokazanego powyżej;
• b' jest rzutem krawędzi b na przeciwprostokątną;
• c' jest rzutem krawędzi c na przeciwprostokątną;
• h jest wysokością trójkąta prostokątnego poprowadzoną od wierzchołka kąta prostego A w dół do przeciwprostokątnej BC.

Przykład 1: Dany jest trójkąt ABC prostokątny przy punkcie A i o wysokości AH. Oblicz BC, AC, AH wiedząc, że AB = 15 cm, HC = 16 cm.

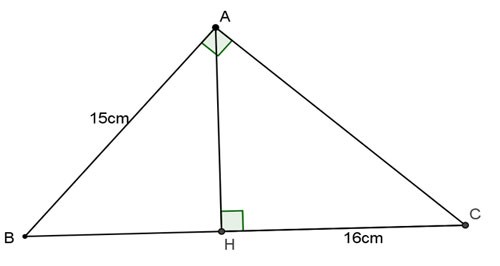
Nagroda:

Stosując wzór algebraiczny w trójkącie prostokątnym ABC otrzymujemy:

AC2 = CH.BC = 16.BC

Zgodnie z twierdzeniem Pitagorasa dla trójkąta prostokątnego ABC o kącie prostym A mamy:

AB2 + AC2 = BC2

⇔ 152 + 16.p.n.e. = 2 p.n.e.

⇔ BC2 - 16.p.n.e. - 225 = 0

⇔ p.n.e.2 - 25.p.n.e. + 9.p.n.e. - 225 = 0

⇔ BC (BC - 25) + 9 (BC - 25) = 0

⇔ (p.n.e. - 25)(p.n.e. + 9) = 0

⇔ BC = 25 lub BC = -9 (wyeliminuj)

⇒ AC2 = 16.BC = 16,25 = 400 ⇒ AC = 20 (cm)

Rozważ trójkąt prostokątny ABC, w którym: AH.BC = AB.AC (wzór geometryczny)

=> AH = AB.AC/BC = 15,20/25 = 12(cm)

Tak więc BC=25(cm); AC=20(cm); AH=12(cm)

Przykład 2 :

Dany trójkąt ABC jest prostokątny przy punkcie A, AB=24cm, AC=32cm. Symetralna odcinka BC przecina AC, BC odpowiednio w punktach D i E. Oblicz DE.

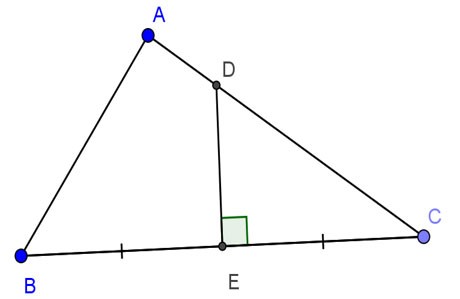
Nagroda:

Rozważmy trójkąt prostokątny ABC. Mamy:

BC2 = AB2 + AC2 (zgodnie z twierdzeniem Pitagorasa)

BC2 = 242+322

BC2 = 1600

BC = 40(cm)

EC = BC : 2 = 40 : 2 = 20 (cm)

Rozważ trójkąt prostokątny ACB i trójkąt prostokątny ECD z:

Jest ∠A = ∠E = 90o

∠C wspólne

=> Trójkąt ACB ∾ trójkąt ECD (gg)

=> AC/EC = AB/ED

=> ED = AB.EC/AC = 15cm

Więc ED = 15 cm

Wzór na obliczenie wysokości w trójkącie równoramiennym

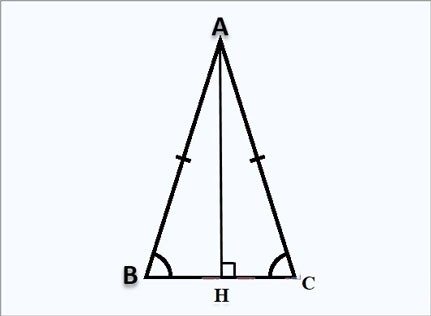
Załóżmy, że mamy trójkąt równoramienny ABC w punkcie A, wysokość AH jest prostopadła do punktu H, jak pokazano powyżej:

Wzór na obliczenie wysokości AH:

Ponieważ trójkąt ABC jest równoramienny w punkcie A, wysokość AH jest również środkową, zatem:

⇒ HB=HC= ½BC

Stosując twierdzenie Pitagorasa do trójkąta prostokątnego ABH dokładnie w punkcie H otrzymujemy:

AH²+BH²=AB²

⇒AH²=AB²−BH²

Na przykład : Dany jest Δ ABC zrównoważony w punkcie A z BC = 30(cm), wysokość AH = 20(cm). Oblicz wysokość odpowiadającą bokowi tego trójkąta równoramiennego.

Rozwiązanie: Załóżmy, że Δ ABC jest równoramienny w punkcie A, gdzie BC = 30(cm)

⇒ BH = CH = 15(cm).

Stosując twierdzenie Pitagorasa mamy:

Teraz musimy obliczyć BK = ?

Mamy:

Z drugiej strony

Dlatego mamy ⇔

Definicja wysokości w trójkącie

Wysokość w trójkącie to odcinek prostopadły, poprowadzony od wierzchołka do przeciwległego boku. Przeciwległą stronę nazywamy podstawą odpowiadającą wysokości. Długość wysokości to odległość między szczytem i dołem.

Właściwości trzech wysokości trójkąta

Trzy wysokości trójkąta przechodzą przez ten sam punkt. Ten punkt nazywa się ortocentrum trójkąta .

Aby móc obliczyć wysokość trójkąta, wystarczy obliczyć nieznane składniki w powyższych wzorach służących do obliczania wysokości trójkąta.

• Na czym się skupiamy? Wzór na obliczenie środka ciężkości trójkąta