Wzór na obliczenie objętości graniastosłupa pionowego, kształt graniastosłupa

Graniastosłup jest wielokątem, który ma dwie równoległe i równe podstawy oraz ściany boczne będące równoległobokiem.

Komentarz:

• Ściany boczne graniastosłupa są równe i równoległe do siebie.
• Ściany boczne są równoległobokami.
• Dwie podstawy graniastosłupa są dwoma równymi wielokątami.

Jaki jest wzór na obliczenie objętości graniastosłupa (pryzmat V) i jaki jest wzór na obliczenie objętości graniastosłupa pionowego? Więcej szczegółów znajdziesz w artykule poniżej.

Spis treści

• 1. Objętość graniastosłupa pionowego
• 3. Klasyfikacja pryzmatów
  • Pryzmat regularny
  • Pryzmat prawy
• 4. Przykład obliczenia objętości graniastosłupa pionowego 

1. Objętość graniastosłupa pionowego

Wzór na obliczenie objętości graniastosłupa pionowego:

Objętość graniastosłupa prostego jest równa iloczynowi pola podstawy i wysokości.

Tam

• Vto objętość graniastosłupa (jednostka m3)
• Bjest to powierzchnia bazowa (jednostka m2)
• hjest wysokością graniastosłupa (jednostka m)

3. Klasyfikacja pryzmatów

Pryzmat regularny

Jest to graniastosłup pionowy, którego podstawą jest wielokąt foremny. Wszystkie ściany boczne graniastosłupa są jednakowymi prostokątami. Na przykład: graniastosłup prawidłowy trójkątny, czworokąt prawidłowy... wtedy rozumiemy go jako graniastosłup prawidłowy.

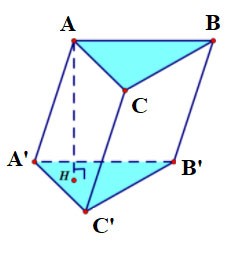
Prawidłowy czworokąt w podstawie nazywa się graniastosłupem prawidłowym czworokątnym.

Pryzmat trójkątny

• Graniastosłup trójkątny ma 5 ścian, 9 krawędzi i 6 wierzchołków.
• Obie podstawy są trójkątne i równoległe do siebie; Każda ściana boczna jest prostokątem;
• Boki są równe;
• Wysokość graniastosłupa trójkątnego jest równa długości jednego boku.

Na przykład:

Graniastosłup trójkątny ABC.A'B'C' ma:

- Dolna podstawa jest trójkątem ABC, a górna podstawa jest trójkątem A'B'C';

Ściany boczne są prostokątami: AA'B'B, BB'C'C, CC'A'A;

- Krawędzie:

• Krawędzie podstawy: AB, BC, CA, A'B', B'C', C'A'
• Boki: AA', BB', CC';

- Wierzchołki: A, B, C, A', B', C'.

- Wysokość to długość jednego boku: AA' lub BB' lub CC'.

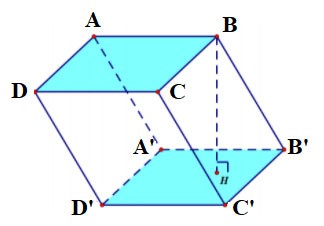
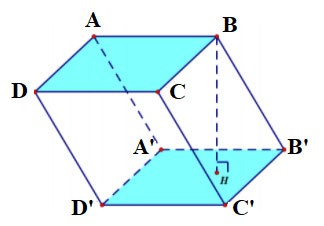
Graniastosłup czworokątny

- Graniastosłup czworokątny ma 6 ścian, 12 krawędzi i 8 wierzchołków.

- Obie podstawy są czworokątami i są do siebie równoległe. Każda ściana boczna jest prostokątem.

- Boki są równe.

- Wysokość graniastosłupa czworokątnego jest równa długości jednego boku.

Na przykład:

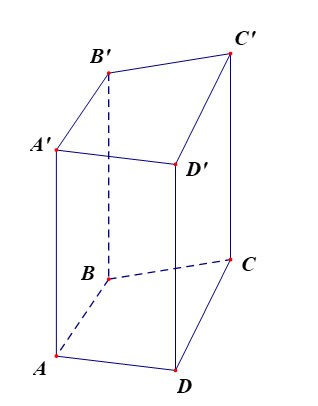
Graniastosłup czworokątny ABCD.A'B'C'D' ma:

- Dolna podstawa jest czworokątem ABCD, górna podstawa jest czworokątem A'B'C'D';

Ściany boczne są prostokątami: AA'B'B, BB'C'C, CC'D'D, DD'A'A;

- Krawędzie:

+ Krawędzie podstawy: AB, BC, CD, DA, A'B', B'C', C'D', D'A'

+ Krawędzie boczne: AA', BB', CC', DD' są równe.

- Wierzchołki: A, B, C, D, A', B', C', D'.

- Wysokość to długość jednego boku: AA' lub BB' lub CC' lub DD'.

Uwaga: Graniastosłupy prostokątne i sześciany są również graniastosłupami czworokątnymi.

Pryzmat prawy

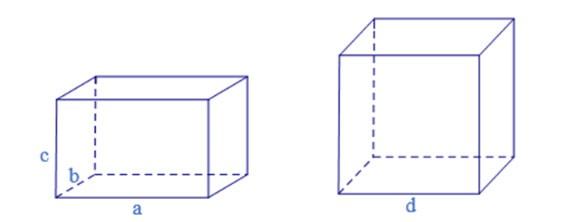
Jeżeli graniastosłup ma krawędzie boczne prostopadłe do podstawy, nazywa się go graniastosłupem prostym.

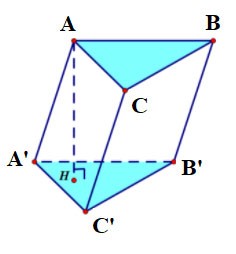
Notatka:

Jeżeli podstawą czworokąta jest prostokąt, pionowy walec czworokąta nazywany jest pudełkiem prostokątnym.

Jeśli czworokątny walec ma 12 boków o długości a, to nazywa się sześcianem.

Porównaj pryzmat prawy i pryzmat zwykły:

4. Przykład obliczenia objętości graniastosłupa pionowego

Przykład 1: 

Dany jest graniastosłup ABC.A'B'C', którego podstawą ABC jest trójkąt równoboczny o boku a = 2 cm i wysokości h = 3 cm. Oblicz objętość tego graniastosłupa?

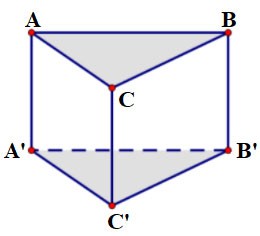
Nagroda:

Ponieważ podstawą jest trójkąt równoboczny o boku a, pole wynosi:

W tym momencie objętość graniastosłupa wynosi:

Przykład 2: 

Ćwiczenie 1: Dany jest pionowy pojemnik o krawędziach AB = 3a, AD = 2a, AA'= 2a. Oblicz objętość bloku A'.ACD'

Polecić:

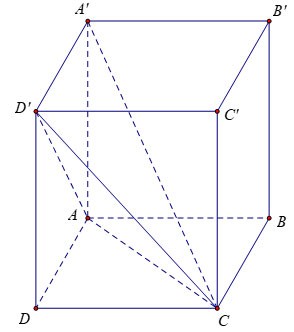
Ponieważ ściana boczna ADD'A' jest prostokątem, mamy:

Przykład 3 : Dany jest graniastosłup pionowy ABC.A'B'C', którego podstawą jest trójkąt równoboczny o boku a√3, kąt między podstawą a graniastosłupem wynosi 60º. Niech M będzie środkiem odcinka BB'. Oblicz objętość ostrosłupa M.A'B'C'.

Nagroda:

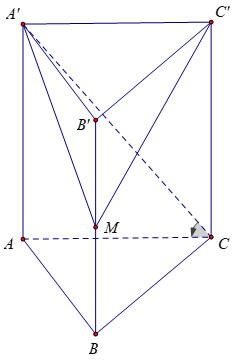
Dlatego możemy wnioskować, że

Mamy:

Przykład 4: 

Dany jest prawidłowy czworokątny graniastosłup ABCD.A'B'C'D', którego krawędź podstawy ma długość a, a ściana (DBC') tworzy z podstawą ABCD kąt 60º. Oblicz objętość graniastosłupa ABCD.A'B'C'D?

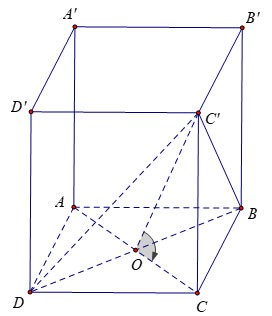
Mamy: w środku O kwadratu ABCD.

Z drugiej strony zatem

Wywnioskować

Również:

Przykład 5: 

Oblicz objętość V sześcianu ABCD.A'B'C'D', wiedząc, że AC'=a√3

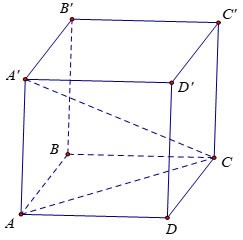
Nagroda:

Niech x będzie długością boku sześcianu.

Rozważ trójkąt AA'C prostokątny w punkcie A, w którym:

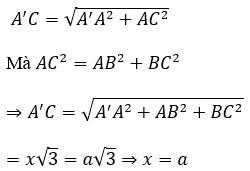
Zatem objętość sześcianu wynosi V=a^3.

Oprócz powyższego wzoru na obliczenie objętości graniastosłupa, możesz zapoznać się z innymi artykułami na temat wzoru na obliczenie objętości bryły obrotowej , wzoru na obliczenie pola i obwodu koła ...