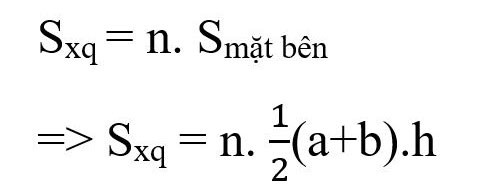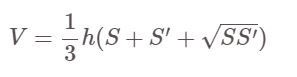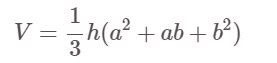Wzór na obliczenie objętości ostrosłupa ściętego, pola powierzchni bocznej i pola całkowitego ostrosłupa ściętego

W poniższym artykule dowiesz się, czym jest ostrosłup ścięty, jak obliczyć objętość ostrosłupa ściętego, pole powierzchni bocznej i pole całkowite ostrosłupa ściętego.

Spis treści

• Definicja ściętego stożka
  • Właściwości ściętego ostrosłupa:
• Wzór na obliczenie pola ostrosłupa ściętego
  • Powierzchnia ściętego ostrosłupa 
  • Całkowita powierzchnia ściętego ostrosłupa
• Wzór na obliczenie objętości ostrosłupa ściętego

Definicja ściętego stożka

Ostrosłup ścięty jest częścią wielościanu, położoną między podstawą a przekrojem poprzecznym przeciętym płaszczyzną równoległą do podstawy ostrosłupa.

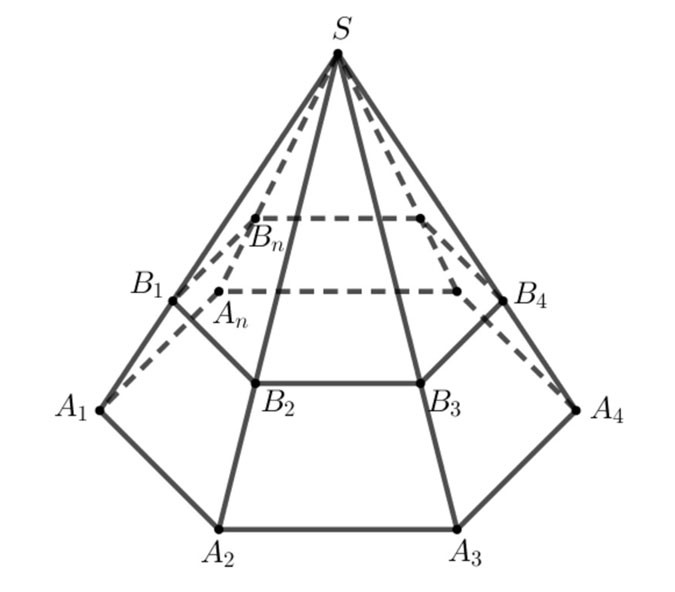
• Figura składająca się z wielokątów A1A2...An,B1B2...BnA1A2...An,B1B2...Bn i trapezów A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn nazywana jest ostrosłupem ściętym i oznaczana jest jako A1A2...An.B1B2...Bn.A1A2...An.B1B2...Bn.
• Mówiąc prościej, ścięta piramida powstaje z piramidy S.A1A2...AnS.A1A2...An po odcięciu piramidy S.B1B2...Bn.S.B1B2...Bn.

+ Wielokąty A1A2...An,B1B2...BnA1A2...An,B1B2...Bn nazywane są dwiema podstawami,

+ Trapezy A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn nazywane są ścianami bocznymi.

+ Odcinki A1B1,A2B2,...,AnBnA1B1,A2B2,...,AnBn nazywane są krawędziami bocznymi, krawędzie powierzchni podstawy nazywane są krawędziami podstawy.

+ Odległość między dwiema podstawami nazywamy wysokością ściętego ostrosłupa.

Właściwości ściętego ostrosłupa:

• Dwie podstawy to dwa wielokąty (trójkąty, czworokąty, pięciokąty itp.) z odpowiednimi bokami równoległymi i równymi stosunkami odpowiednich boków.
• Wszystkie ściany boczne są trapezami.
• Linie zawierające krawędzie boczne zbiegną się w jednym punkcie (na szczycie piramidy).
• Ostrosłup ścięty to ostrosłup, którego podstawą jest wielokąt foremny (o równych bokach). Zatem wszystkie ściany boczne ściętego ostrosłupa są jednakowymi trapezami.

Wzór na obliczenie pola ostrosłupa ściętego

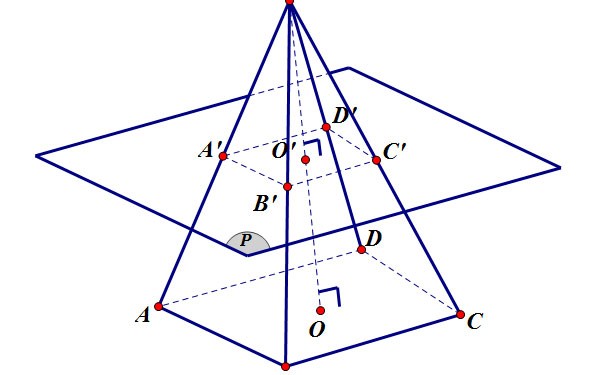
Powierzchnia ściętego ostrosłupa

Pole boczne ostrosłupa ściętego to pole otaczających go ścian, część otaczająca ostrosłup ścięty, z wyłączeniem pola obu podstaw.

Jak obliczyć pole powierzchni bocznej ostrosłupa ściętego: Oblicz pole każdej ściany bocznej (trapezu) ostrosłupa ściętego według wzoru na pole trapezu normalnego , a następnie oblicz pole całkowite.

Wzór na obliczenie pola prawidłowego ostrosłupa ściętego:

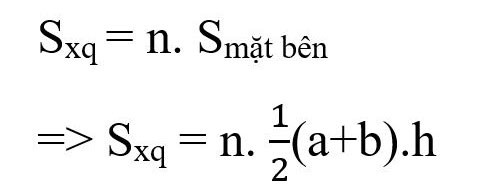
Tam:

• Sxq: okolica
• n: liczba ścian bocznych ściętego ostrosłupa (równa liczbie krawędzi wielokąta podstawy)
• a, b: długości boków odpowiednio górnej i dolnej podstawy
• h: wysokość czworokątów bocznych.

Przykład 1: 

Oblicz pole boczne ściętego ostrosłupa prawidłowego czworokątnego o krawędziach podstawy wynoszących 10 cm i 15 cm i wysokości boku wynoszącej 12 cm.

Nagroda: 

Ściana boczna ostrosłupa prawidłowego czworokątnego ściętego jest trapezem równoramiennym, więc pole jednej ściany bocznej wynosi:

Prawidłowa czworokątna ścięta ostrosłupowa ma 4 równe ściany, więc jej pole boczne wynosi:

150 x 4 = 600 (cm2)

Przykład 2: Oblicz pole boczne ściętego ostrosłupa prawidłowego czworokątnego o krawędziach podstawy wynoszących 6cm i 8cm i wysokości boku wynoszącej 5cm. Oblicz pole boczne ściętego ostrosłupa prawidłowego czworokątnego o krawędziach podstawy wynoszących 6cm i 8cm.

Nagroda: 

Boczna ściana ostrosłupa prawidłowego czworokątnego ściętego jest trapezem równoramiennym, więc pole jednej ściany bocznej jest równe

Prawidłowa czworokątna ścięta ostrosłupowa ma cztery równe boki, więc jej pole boczne jest równe

35 x 4 = 140 (cm2)

Całkowita powierzchnia ściętego ostrosłupa

Całkowite pole powierzchni ostrosłupa ściętego jest równe sumie pola powierzchni bocznej i pola obu podstaw.

Wzór:                    Stp = Sxq + Duże dno + Małe dno

Tam:

• Stp: Powierzchnia całkowita
• Sxq: Okolica
• Duża podstawa: Duża powierzchnia podstawy
• Mała baza: Mała powierzchnia bazy

Na przykład: 

Oblicz pole całkowite prawidłowego ostrosłupa ściętego na podstawie wymiarów podanych na rysunku.

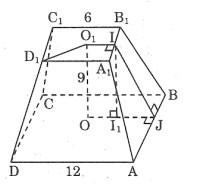
Nagroda:

Mamy:

12 lat temu ⇒ 6 lat temu

Narysuj II1 ⊥ OJ mamy: I1J = 3

Stosując twierdzenie Pitagorasa do trójkąta prostokątnego II1J otrzymujemy:

IJ2 = II12 + I1J2 = 92 + 32 = 90

Stąd:

Pole jednego boku trapezu wynosi:

Powierzchnia otoczenia wynosi:

Pole podstawy górnej wynosi: S = 6 x 6 = 36 (jednostek)

Pole podstawy dolnej wynosi: S = 12 x 12 = 144 (jednostek)

Całkowite pole ostrosłupa ściętego jest równe:

Wzór na obliczenie objętości ostrosłupa ściętego

Przepis:

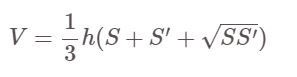
Tam:

• V: objętość ściętego ostrosłupa
• S, S' to odpowiednio pola większej i mniejszej podstawy piramidy.
• h: wysokość piramidy, czyli odległość między dwiema dużymi i małymi podstawami

Czy ostrosłup ścięty jest kwadratem (czworokątem foremnym):

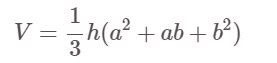
Tam:

• V: Objętość
• h: Wysokość piramidy
• a, b to długości krawędzi odpowiednio dużej podstawy i małej podstawy.