Wzór na obliczenie pola rombu, obwód rombu

Przypomnijmy i zapamiętajmy wzór na obliczenie pola, obwodu i przekątnej rombu w poniższym artykule.

Spis treści

• 1. Wzór na obliczenie pola rombu
  • Wzór na obliczenie pola rombu na podstawie podstawy i wysokości
  • Wzór na obliczenie pola rombu na podstawie wzoru trójkąta (jeśli znasz kąt rombu)
• 2. Wzór na obliczenie obwodu rombu
• 3. Co to jest romb?
  • Właściwości rombu
• 4. Przykład obliczania pola i obwodu rombu

1. Wzór na obliczenie pola rombu

Pole rombu mierzy się wielkością pola powierzchni, czyli widoczną płaską częścią rombu.

Wzór na obliczenie pola rombu na podstawie podstawy i wysokości

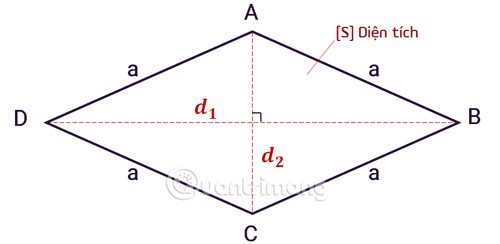
Pole rombu jest równe połowie iloczynu długości dwóch przekątnych , wzór jest następujący:

Tam:

• Sjest polem rombu.
• d1i d2są dwiema przekątnymi rombu.

Przykład obliczenia pola rombu.

Lekcja 1: Jest kawałek tektury w kształcie rombu, którego dwie przecinające się przekątne mają długość odpowiednio 6 cm i 8 cm. Jakie jest pole powierzchni tektury w kształcie rombu?

Stosując metodę obliczania pola rombu, mamy d1 = 6 cm i d2 = 8 cm. Podstawiamy to do wzoru i otrzymujemy następujący wynik:

S = 1/2 x (d1 x d2) = 1/2 (6 x 8) = 1/2 x 48 = 24 cm2

Wzór na obliczenie pola rombu na podstawie wzoru trójkąta (jeśli znasz kąt rombu)

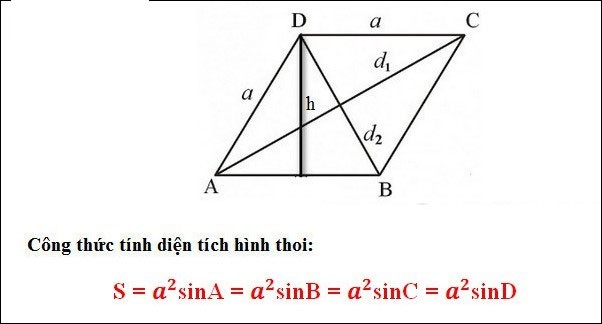
W którym: a: ​​bok rombu

Przykład 1 : Dany jest romb ABCD, którego krawędź wynosi 4 cm, a kąt A = 35 stopni. Oblicz pole rombu ABCD.

Rozwiązanie: Stosując wzór, mamy a = 4, kąt = 35 stopni. Zastępujemy formułę w następujący sposób:

S = a2 x sinA = 42 x sin(35) = 9,176 (cm2)

2. Wzór na obliczenie obwodu rombu

Obwód rombu oblicza się poprzez dodanie długości linii otaczających figurę, która jest również linią otaczającą cały obszar.

Aby obliczyć obwód rombu, należy obliczyć sumę długości czterech boków. Szczegółowy wzór wygląda następująco:

Tam:

• Pjest obwodem rombu.
• ajest długością boku rombu.

Na przykład: Dany jest romb ABCD o równych długościach boków i długości 7 cm. Jaki jest obwód tego rombu?

Zgodnie ze wzorem na obwód rombu przedstawionym powyżej, a = 7 cm. Zatem obwód rombu ABCD obliczymy następująco:

P (ABCD) = oś 4 = 7 x 4 = 28 cm

3. Co to jest romb?

Romb jest czworokątem, który ma cztery równe boki. Jest to równoległobok, który ma dwa sąsiednie boki równe lub równoległobok, który ma dwie przekątne prostopadłe do siebie.

Właściwości rombu

• 2 równe przeciwległe kąty
• Dwie przekątne są prostopadłe do siebie i przecinają się w środku każdej linii.
• Dwie przekątne są dwusiecznymi kątów.

W tym artykule Quantrimang.com przedstawi skuteczne wzory na obliczanie pola i obwodu rombu, które mogą przydać się w nauce i pracy.

4. Przykład obliczania pola i obwodu rombu

Przykład 1: 

Dany jest romb ABCD o boku AD = 4m i kącie DAB = 30 stopni. Oblicz pole rombu ABCD.

Nagroda:

Ponieważ ABCD jest rombem, powstałe trójkąty są trójkątami równoramiennymi. Niech I będzie środkiem dwóch przekątnych, tak aby AI była prostopadła do BD, a kąt IAB = 15 stopni.

Zatem AI = AB. cos IAB = 4. Cos 15 = 3,84 m.

Rozważmy trójkąt prostokątny ABI. Zgodnie z twierdzeniem Pitagorasa mamy:

BI2= AB2- AI2= 1,25m

Więc BI = 1,1m

AC = 2. AI = 7,68 m

BD = 2. BI = 2,2m

Na podstawie wzoru na obliczenie pola rombu mamy pole rombu ABCD = ½. AC. BD = 8,45(m2)

Przykład 2: Mając romb o boku długości 6 cm i jednym z jego kątów równym 60°, oblicz pole rombu.

Dane te nie będą podstawą do obliczenia pola rombu. Aby obliczyć przekątną rombu, będziesz musiał wykorzystać właściwości rombów i trójkątów równobocznych , a także nauczyć się, jak obliczać boki w trójkącie prostokątnym. Kroki są następujące:

Krok 1: Narysuj obrazek i zanotuj znane fakty.

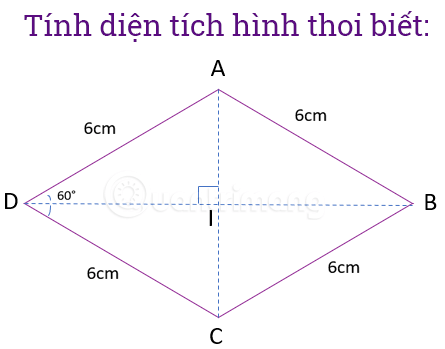
Krok 2: Stosując własności rombu mamy:

, przekątna AC jest dwusieczną kąta A, więc kąt będzie równy 1/2 kąta i równy 60°. (Suma kątów wewnętrznych czworokąta wynosi 360°, suma kątów wewnętrznych trójkąta wynosi 180°). Zatem trójkąt ADC będzie trójkątem równobocznym => bok AC ma 6 cm. I jest punktem środkowym AC => AI=3cm.

Krok 3: Oblicz długość DI

Trójkąt DIA jest prostokątny przy I, bok DI oblicza się następująco:

=> cm

Krok 4: Oblicz pole rombu ABCD:

Przykład 3: Dany jest romb ABCD o boku 13 cm, dwie przekątne przecinają się w punkcie H.

Oblicz pole rombu ABCD wiedząc, że pole BH jest półtora raza większe od pola AH.

Rozwiązanie:

ABCD jest rombem, więc trójkąt AH jest prostopadły do ​​BH w punkcie H, a następnie trójkąt ABH jest prostokątny w punkcie H.

Niech BH = 2a, wówczas AH = 3a.

Zgodnie z twierdzeniem Pitagorasa mamy: AH²+ BH²= AB² ⇒9a²+4a²=13 ⇒13a²=13 ⇒a=1

Dlatego AH = 3 cm, BH = 2 cm lub AC = 6 cm, BD = 4 cm

Pole rombu wynosi: S = 6,4/2 = 12cm².

Przykład 4 :

Dany jest romb MNPQ, kąt A = 30o, obwód = 20m, środek przekątnej wynosi I. Jakie jest pole rombu MNPQ?

Rozwiązanie

Długość boku rombu wynosi a = P : 4 = 20 : 4 = 5m

Ponieważ trójkąty utworzone przez romby są trójkątami równoramiennymi, trójkąt utworzony ze środka przekątnej I, punktów M, N zostanie utworzony przez kąt IMN = 15o

Długość połowy przekątnej MI = MN x cos IMN = 5 x cos150 = 4,8 m

Stosując twierdzenie Pitagorasa w trójkącie prostokątnym MNI otrzymujemy: NI = 1,4m

Długość przekątnej NQ = 2 x NI = 2 x 1,4 = 2,8 m

Pole rombu MNPQ wynosi S = 2 x ½ x NQ x MI = 1 x ½ x 2,8 x 4,8 = 13,44 m2

Odpowiedź: 13,44 m2

Jeśli masz jakiekolwiek pytania dotyczące wzoru na obliczenie pola i obwodu rombu, zostaw komentarz poniżej, abyśmy mogli wspólnie je omówić i odpowiedzieć. Dziękujemy za śledzenie artykułu.