Wzór na obliczenie powierzchni i objętości kuli

W poniższym artykule zapoznamy się ze wzorem na obliczanie pola powierzchni i objętości kuli za pomocą serwisu Quantrimang.com i omówimy go.

Spis treści

• Czym jest kula?
  • Czym jest kula?
• Wzór na obliczenie powierzchni i objętości kuli
  • Wzór na obliczenie powierzchni kuli
  • Wzór na obliczenie objętości kuli:
• Wzór na obliczenie promienia kuli
  • Kula opisana na piramidzie ma bok prostopadły do ​​podstawy.
  • Czworościan kwadratowy (jest to szczególny przypadek wzoru 1)
  • Podstawą graniastosłupa prawidłowego pionowego jest wielokąt wpisany.
  • Wzór na czworościan, którego wierzchołki są wierzchołkami graniastosłupa prostego
  • Wzór na obliczenie promienia kuli dla ostrosłupa, którego ściany boczne są prostopadłe do podstawy
• Przykłady obliczania powierzchni i objętości kuli

Czym jest kula?

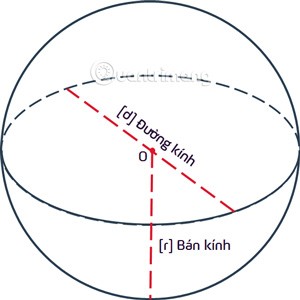
Kula to zbiór punktów równoodległych od danego punktu stałego O rw przestrzeni trójwymiarowej. Punkt O nazywamy środkiem, a odległość rod niego promieniem kuli.

Czym jest kula?

Kula to zbiór punktów leżących wewnątrz kuli. Kulą nazywamy kulę lub kulę o środku O i promieniu r = OA.

Wzór na obliczenie powierzchni i objętości kuli

Wzór na obliczenie powierzchni kuli

Powierzchnia kuli jest czterokrotnie większa od powierzchni dużego koła, która jest czterokrotnie większa od stałej Pi pomnożonej przez kwadrat promienia kuli.

Wzór na obliczenie objętości kuli:

Objętość kuli, zwana również objętością kuli, oblicza się poprzez pomnożenie trzech czwartych liczby Pi przez sześcian promienia kuli.

Tam:

• Sjest powierzchnią kuli
• Vjest objętością kuli
• rjest promieniem kuli/sfery
• djest kulą/kulą

Wzór na obliczenie promienia kuli

Kula opisana na piramidzie ma bok prostopadły do ​​podstawy.

• Rd jest promieniem podstawy.
• h jest długością boku prostopadłego do podstawy.

Na przykład : Dany jest ostrosłup S.ABCD o podstawie prostokątnej, gdzie AB = 3a, BC = 4a, SA = 12a i SA prostopadły do ​​podstawy. Oblicz promień R kuli opisanej na ostrosłupie S.ABCD.

Rozwiązanie: Mamy

Więc

Czworościan kwadratowy (jest to szczególny przypadek wzoru 1)

Kwadratowy blok OABC ma OA, OB, OC prostopadłe do siebie i ma:

Na przykład:

Czworościan OABC ma OA, OB, OC, które są wzajemnie prostopadłe i ma opisaną sferę o promieniu . Największa objętość czworościanu OABC

Rozwiązanie : Mamy

Z drugiej strony mamy:

Zgodnie z nierównością AM-GM mamy:

Podstawą graniastosłupa prawidłowego pionowego jest wielokąt wpisany.

Tam:

• Rd to promień podstawy
• h jest długością boku.

Przykład 1: Dana jest kula o promieniu R opisana na sześcianie o boku a. Które z poniższych stwierdzeń jest prawdziwe?

A.

B.

C.

D.

Rozwiązanie: Mamy

Odpowiedź brzmi zatem C.

Wzór na czworościan, którego wierzchołki są wierzchołkami graniastosłupa prostego

Czworościan (H1) ma wierzchołki, które są wierzchołkami graniastosłupa pionowego (H2), zatem:

Wzór na obliczenie promienia kuli dla ostrosłupa, którego ściany boczne są prostopadłe do podstawy

W którym R, d jest promieniem podstawy; a, x to odpowiednio długość przecięcia ściany bocznej i podstawy, kąt między górną krawędzią ściany bocznej, patrząc w dół na podstawę.

Możesz też użyć wzoru

Gdzie: Rb jest promieniem opisanym na ścianie bocznej, a a jest długością przecięcia ściany bocznej i podstawy.

Na przykład: 

Dany jest ostrosłup S.ABCD o podstawie kwadratu, trójkąt równoboczny SAD o boku √2a i leżący w płaszczyźnie prostopadłej do podstawy. Oblicz promień R kuli opisanej na ostrosłupie S.ABCD.

A.

B.

Rozwiązanie: Mamy

Więc poprawna odpowiedź to B.

Przykłady obliczania powierzchni i objętości kuli

Lekcja 1 : Dany jest okrąg o obwodzie 31,4 cm. Oblicz objętość kuli, której promień jest równy promieniowi danego okręgu.

Nagroda:

Obwód koła C = 2πr = 31,4 cm

=> Promień r = C/2π = 5 cm

Objętość danej kuli wynosi:

V = ⁴⁄₃πr³ = 4/3.3.14.(5)³ = 523,3 cm3

Lekcja 2 : Oblicz objętość kuli o średnicy d = 4 cm.

Nagroda:

Promień r = d/2 = 2 cm

Objętość kuli wynosi:

V = ⁴⁄₃πr³ = 4/3.3.14.(2)³ = 33,49 cm3

Lekcja 3 :

Niech okrąg o średnicy 4a obraca się wokół swojej średnicy. Jaka jest zatem objętość obracającego się ciała stałego?

Rozwiązanie: Biorąc pod uwagę okrąg o średnicy 4a obracający się wokół swojej średnicy, otrzymujemy kulę o średnicy 4a lub promieniu R = 2a.

Objętość kuli wynosi:

Lekcja 4 :

Kula o promieniu R√3 ma pole:

A.4√3πR2

B.4πR2

C.6πR2

D.12πR2

Rozwiązanie: Zastosuj wzór: S = 4πR2

Powierzchnia kuli o promieniu R√3 wynosi: S = 4π(R√3)2 = 12πR2

Odpowiedź brzmi zatem D.

Dwie krótkie formuły, ale zapamiętanie ich na dłużej jest bardzo trudne. Dodaj artykuł do zakładek i otwórz go, gdy będzie Ci potrzebny. Mam nadzieję, że ten artykuł będzie dla Ciebie przydatny.

Oprócz wzoru na obliczenie pola powierzchni i objętości kuli, możesz również skorzystać ze wzoru na obliczenie pola niektórych innych podstawowych figur, takich jak trójkąty , prostokąty i równoległoboki. ..