System dziesiętny (podstawa 10)
System dziesiętny jest standardowym i najpowszechniej stosowanym systemem w życiu codziennym. W tym systemie liczenia podstawą jest liczba 10. System dziesiętny składa się z 10 znaków, którymi są cyfry od 0 do 9. Dokładniej rzecz biorąc, są to: 0, 1, 2, 3, 4, 5, 6, 7, 8 i 9.
System dziesiętny jest jednym z najstarszych znanych systemów liczbowych i był używany przez wiele starożytnych cywilizacji. Trudność w przedstawianiu bardzo dużych liczb w systemie dziesiętnym została przezwyciężona dzięki hindusko-arabskiemu systemowi liczbowemu. Hindusko-arabski system liczbowy określa pozycje cyfr w liczbie. Każda pozycja odpowiada potędze liczby 10, zaczynając od pozycji najdalej na prawo przed przecinkiem dziesiętnym, czyli 100.
Na przykład liczba 2345,67 w systemie dziesiętnym:
Dlatego liczbę 2345,67 można również przedstawić jako: (2 * 103) + (3 * 102) + (4 * 101) + (6 * 10-1) + (7 * 10-2).
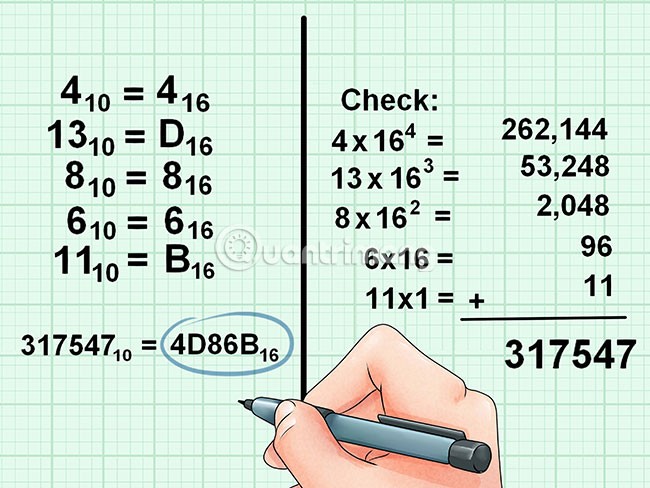
Przykład zamiany systemu dziesiętnego na szesnastkowy:
Szesnastkowy (podstawa 16)
System liczbowy szesnastkowy (Hexadecymalny), zwany również systemem szesnastkowym (Hexadecymalnym) wykorzystuje system liczbowy o podstawie szesnastkowej i jest popularnym wyborem do reprezentowania długich wartości binarnych, ponieważ jego format jest znacznie bardziej zwarty i łatwiejszy do zrozumienia niż długie ciągi binarne składające się tylko z dwóch wartości: 1 i 0.
Tabela konwersji systemu 10 na system 16
| System dziesiętny | System szesnastkowy |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | mi |
| 15 | F |
Zobacz także:
Masz problem z logowaniem przez Internet w Microsoft Teams? Uzyskaj natychmiastowe rozwiązania typowych problemów, takich jak „Coś poszło nie tak” lub „Logowanie się zapętla”. Przewodnik krok po kroku, jak rozwiązać problemy z logowaniem przez Internet w Teams i zachować produktywność. Zaktualizowano o najnowsze poprawki przeglądarki.
Masz problem z błędem w samouczku Microsoft Teams? Odkryj proste rozwiązania krok po kroku, aby szybko go rozwiązać. Wyczyść pamięć podręczną, zaktualizuj i wiele więcej, aby zapewnić płynną pracę zespołową. Zaktualizowano do najnowszych wersji!
Masz dość błędów odtwarzania multimediów w Microsoft Teams, które psują Twoje spotkania w 2026 roku? Skorzystaj z naszego eksperckiego przewodnika krok po kroku, aby szybko naprawić błędy dźwięku, obrazu i udostępniania – bez konieczności posiadania umiejętności technicznych. Bezproblemowa współpraca czeka!
Masz problem z błędem proxy w Microsoft Teams? Poznaj sprawdzone sposoby rozwiązywania problemów z ustawieniami proxy w Microsoft Teams. Wyczyść pamięć podręczną, dostosuj ustawienia proxy i wróć do płynnych połączeń w kilka minut dzięki naszemu przewodnikowi eksperta.
Frustruje Cię pętla uruchamiania ekranu powitalnego w Microsoft Teams? Postępuj zgodnie ze sprawdzonymi krokami rozwiązywania problemów z pętlą uruchamiania ekranu powitalnego w Microsoft Teams: wyczyść pamięć podręczną, zresetuj aplikację, zainstaluj ponownie. Wróć do płynnej współpracy w kilka minut!
Frustruje Cię brak pokoi spotkań w Teams? Odkryj najczęstsze powody, dla których nie widzisz pokoi spotkań w Teams i postępuj zgodnie z naszymi krok po kroku, aby w kilka minut uruchomić je płynnie. Idealne rozwiązanie zarówno dla organizatorów, jak i uczestników!
Napotkałeś dziś błąd w Microsoft Teams? Ten przewodnik krok po kroku dotyczący rozwiązywania problemów z Microsoft Teams ujawnia pierwsze kroki, które pozwolą szybko go rozwiązać. Szybkie poprawki dotyczące łączności, pamięci podręcznej i aktualizacji, które pozwolą Ci bezproblemowo wrócić do czatowania.
Frustruje Cię brak dodatku Microsoft Teams w Outlooku? Odkryj najważniejsze przyczyny i proste rozwiązania krok po kroku, aby bezproblemowo przywrócić płynną integrację Teams z Outlookiem. Działa z najnowszymi wersjami!
Odblokuj dokładne lokalizacje kluczy rejestru Microsoft Teams w systemie Windows 11. Przewodnik krok po kroku, jak je znaleźć, uzyskać do nich dostęp i bezpiecznie je modyfikować, aby zapewnić optymalną wydajność i rozwiązywać problemy. Niezbędny dla specjalistów IT i entuzjastów Teams.
Masz dość błędów skrótów w Microsoft Teams, które blokują Twój przepływ pracy? Poznaj sprawdzone sposoby na rozwiązanie błędów skrótów i awarii uruchamiania Microsoft Teams, aby zapewnić płynną współpracę. Szybkie i proste rozwiązania w pakiecie!
